Pour un œil non averti, les plantes peuvent sembler pousser de façon plutôt impulsive, sortant des feuilles au hasard pour créer un grand fouillis vert. Regardez de plus près, cependant, et vous constaterez que quelques motifs curieusement réguliers apparaissent dans tout le monde naturel, de la symétrie équilibrée des pousses de bambou aux spirales hypnotisantes des plantes succulentes.
En fait, ces schémas sont suffisamment cohérents pour que des calculs mathématiques rigoureux permettent de prédire assez bien la croissance organique. Une hypothèse qui a joué un rôle central dans l’étude de la phyllotaxie, ou motifs des feuilles, est que les feuilles protègent leur espace personnel. Partant de l’idée que les feuilles déjà existantes ont un effet inhibiteur sur les nouvelles et que les feuilles se développent pour empêcher que d’autres poussent à proximité, les scientifiques ont créé des modèles capables de reconstituer bon nombre des conceptions courantes de la nature. La séquence toujours fascinante de Fibonacci, par exemple, apparaît dans tout, des arrangements de semences de tournesol aux coquilles de nautile en passant par les pommes de pin. Le consensus actuel est que les mouvements de l'hormone de croissance auxine et des protéines qui la transportent à travers une plante sont responsables de ces modèles.
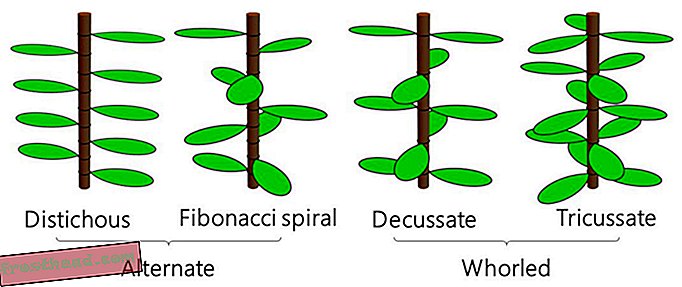La phyllotaxie alternée désigne un arrangement foliaire à une feuille par nœud, tandis que la phyllotaxie verticillée est un arrangement à deux feuilles ou plus par nœud. Les types alternatifs courants sont le phyllotaxis distique (bambou) et le phyllotaxis spiral de Fibonacci (le succulent aloès spiralé), et les types rougis communs sont le phyllotaxis décussé (basilic ou menthe) et le phyllotaxis tricussé ( Nerium oleander, parfois appelé dogbane). (Takaaki Yonekura sous CC-BY-ND) Cependant, certains arrangements de feuilles continuent de bouleverser les modèles populaires de croissance des plantes, notamment les équations de Douady et Couder (connues sous les noms DC1 et DC2) qui dominent depuis les années 1990. Une équipe dirigée par des chercheurs de l'Université de Tokyo et étudiant un arbuste appelé Orixa japonica a constaté que les équations antérieures ne pouvaient pas recréer la structure inhabituelle de la plante. Elle a donc décidé de repenser le modèle lui-même. Leur modèle mis à jour, décrit dans une nouvelle étude de PLOS Computational Biology, non seulement reproduit le modèle jadis insaisissable, mais il peut également décrire d’autres arrangements plus communs mieux que les équations précédentes, selon les auteurs.
«Dans la plupart des plantes, les schémas phyllotactiques ont une symétrie - symétrie spirale ou symétrie radiale», explique le physiologiste des plantes de l'Université de Tokyo, Munetaka Sugiyama, auteur principal de la nouvelle étude. «Mais dans cette plante spéciale, Orixa japonica, le motif phyllotactique n’est pas symétrique, ce qui est très intéressant. Il y a plus de 10 ans, j'ai eu l'idée que certains changements dans le pouvoir inhibiteur de chaque primordium de feuille pourraient expliquer ce schéma particulier. ”
Les botanistes utilisent les angles de divergence, ou angles entre les feuilles consécutives, pour définir la phyllotaxie d'une plante. Alors que la plupart des configurations de feuilles gardent un angle de divergence constant, l'arbuste O. japonica, originaire du Japon et d'autres régions de l'Asie de l'Est, fait pousser les feuilles en alternant quatre angles répétés: 180 degrés, 90 degrés, 180 degrés, puis 270 degrés.
Un arbuste Orixa japonica avec les différents angles de divergence des feuilles visibles. (Qwert1234 via Wikicommons sous CC BY-SA 4.0) Ce motif, que les chercheurs ont qualifié de phyllotaxie «orixée», n’est pas une simple anomalie, les plantes d’autres taxons alternant leurs feuilles séquence compliquée. Étant donné que la disposition des feuilles apparaît à différents endroits de l'arbre évolutif, les auteurs ont conclu que la similitude provenait d'un mécanisme commun qui nécessitait une étude plus approfondie.
Après avoir testé les équations de Douady et Couder avec différents paramètres, les auteurs ont pu produire des motifs proches de la disposition de l'orixate en alternance, mais aucune des plantes simulées ne correspondait parfaitement aux échantillons d' O. Japonica qu'ils avaient disséqués et étudiés. L'équipe a donc construit un nouveau modèle en ajoutant une autre variable aux équations de Douady et Couder: l'âge de la feuille. Les anciens modèles supposaient que le pouvoir inhibiteur des feuilles restait le même dans le temps, mais cette constante n'était «pas naturelle du point de vue de la biologie», dit Sugiyama. Au lieu de cela, l'équipe de Sugiyama a envisagé la possibilité que la force de ces signaux «éloignés» change avec le temps.
Les modèles résultants - que l’équipe appelle modèles élargis de Douady et Couder, EDC1 et EDC2 - ont réussi à recréer, par le biais d’une croissance informatisée, les arrangements foliaires complexes d’ O . japonica . Au-delà de cet exploit, les équations développées ont également produit tous les autres modèles de feuillage courants et ont prédit les fréquences naturelles de ces variétés avec plus de précision que les modèles précédents. Le nouveau modèle EDC2 prédit la «super domination» de la spirale de Fibonacci, en particulier dans le cas des plantes à motifs en spirale, alors que les modèles précédents n’expliquaient pas pourquoi cette forme particulière semble apparaître partout dans la nature.
«Notre modèle, EDC2, peut générer des motifs orixés en plus de tous les principaux types de phyllotaxis. C'est clairement un avantage par rapport au modèle précédent », déclare Sugiyama. «EDC2 s’intègre également mieux à l’occurrence naturelle de divers modèles.»
Feuilles sur une branche d' Orixa japonica (en haut à gauche) et diagramme schématique de la phyllotaxie de l'orixate (à droite). Le modèle orixate affiche un changement particulier de l'angle entre les feuilles sur quatre cycles. Une image au microscope électronique à balayage (centre et en bas à gauche) montre le bourgeon d'hiver d' O. Japonica, où les feuilles commencent à pousser. Les feuilles primordiales sont étiquetées séquentiellement, la plus ancienne étant P8 et la plus jeune, P1. L'étiquette O marque l'apex du tournage. (Takaaki Yonekura / Akitoshi Iwamoto / Munetaka Sugiyama sous CC-BY) Les auteurs ne peuvent pas encore conclure ce qui cause exactement l'âge de la feuille qui affecte ces modèles de croissance, bien que Sugiyama spécule qu'il pourrait avoir un lien avec les changements du système de transport de l'auxine au cours du développement de la plante.
Ciera Martinez, biologiste informaticienne qui n’a pas participé à l’étude, résout de tels mystères. Le modèle des auteurs constitue une étape passionnante vers une meilleure compréhension de la phyllotaxie et laisse la possibilité à d'autres botanistes de combler les lacunes en analysant et en disséquant les plantes.
«Avec les modèles, même si nous ne connaissons peut-être pas encore le mécanisme exact, nous avons au moins des indices puissants sur ce qu'il faut rechercher», explique Martinez dans un courrier électronique. "Nous devons maintenant examiner de plus près les mécanismes moléculaires dans les plantes réelles pour essayer de découvrir ce que le modèle prédit."
Une vue de haut en bas des motifs d'arrangement des feuilles dans la phyllotaxie "orixée" alors que de nouvelles feuilles (demi-cercles rouges) se forment à partir du sommet des pousses (cercle noir central) et se développent vers l'extérieur (Takaaki Yonekura sous CC-BY-ND) L’équipe de Sugiyama s’efforce d’affiner encore son modèle et de le faire générer tous les schémas phyllotactiques connus. Un motif de feuille «mystérieux», une spirale avec un angle de divergence minime, échappe toujours à la prévision informatique, bien que Sugiyama pense qu'ils sont sur le point de craquer le code en feuilles.
«Nous ne pensons pas que notre étude soit pratiquement utile pour la société», déclare Sugiyama. "Mais nous espérons que cela contribuera à notre compréhension de la beauté symétrique de la nature."
