Lorsque la plupart d'entre nous voyons une machine tirer la tire tire sur une promenade touristique, nous pensons au sucre sucré. Jean-Luc Thiffeault pense aux mathématiques douces et douces. En tant que mathématicien appliqué à l'Université de Wisconsin-Madison, Thiffeault s'intéresse particulièrement à la façon dont des matériaux comme le taffy sont mélangés: dans la machine, le bonbon est étiré et replié pour incorporer de l'air et développer sa texture légère et caoutchouteuse. Au fur et à mesure que vous tirez, le rectangle de tire original s’étire de plus en plus, sa longueur augmentant de façon exponentielle à chaque fois. C'est ce ratio qui intéresse Thiffeault.
Contenu connexe
- Chocolat résistant à la fusion, gommes imprimées en 3D et autres brevets de bonbons fascinants
Lorsqu'une personne tire de la tire, elle prend généralement le morceau de bonbon et l'étire sur un crochet pour rapprocher les deux bouts. Ensuite, ils prendront cette pièce pliée et l'étireront à nouveau sur le crochet, en doublant la longueur, etc. En d'autres termes, «la manière humaine de le faire est un facteur de multiplication de 2», dit Thiffeault. Les extracteurs mécaniques peuvent faire mieux, générant souvent des nombres irrationnels exotiques plus importants en tant que facteurs d’étirement.
Il s'avère que le tirage de la tire peut être modélisé par un domaine abstrait des mathématiques appelé dynamique topologique, essentiellement l'étude de changements à long terme et à grande échelle dans le temps dans un espace mathématique. (Si le mot topologique vous semble familier, il a récemment fait les nouvelles du prix Nobel de physique de cette année.) Les mêmes mathématiques qui décrivent le tirage au tire ont également des applications plus sérieuses: de nombreux procédés industriels, notamment le soufflage du verre et la préparation de médicaments, exigent les fluides visqueux doivent être mélangés de manière à ressembler davantage à tirer de la tire que à ajouter de la crème au café. «Si vous essayez de mélanger des objets très visqueux, comme les pâtes de l'industrie pharmaceutique, vous ne pouvez pas vous contenter de les secouer», déclare Thiffeault. "Ce n'est pas comme mélanger de la peinture."
Thiffeault a compris le tirage au sort comme un exemple de mélange visqueux depuis longtemps, mais ce n’est que récemment qu’il s’est penché sur l’histoire des tireurs pour découvrir leurs secrets mathématiques. Le résultat de cette excursion dans les brevets historiques est son article récent «Une histoire mathématique des tireurs de tire», publié sur le serveur de préimpression arXiv en juillet.
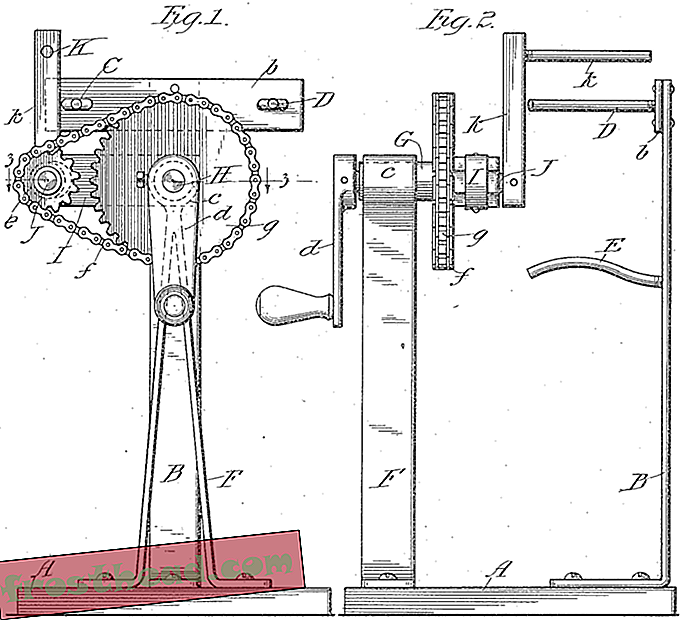Une image d'un brevet de 1916 sur une machine à tire-lait qui apparaît dans l'étude de Thiffeault. Plus précisément, le domaine qui a conduit à sa plongée en profondeur avec tire-tire est l’étude de ce que l’on appelle des cartographies pseudo-Anosov. Pseudo-Anosov est une manière élégante de décrire un processus dans lequel une forme bidimensionnelle est étirée de manière exponentielle dans un sens, alors qu'elle se contracte dans l'autre. Mathématiquement, l'étude des cartographies pseudo-Anosov est relativement nouvelle. «Dans les années 70 et 80, les gens s'efforçaient de trouver des exemples», dit Thiffeault. Ironiquement, ils ont toujours été là pour déposer des brevets sur les tire-tire. "Parce que les mathématiciens n'ont jamais examiné cette littérature, ils n'auraient jamais su qu'ils existaient", dit-il.
Alors qu'il passait au peigne fin aux brevets sur les tire-tire, Thiffeault a trébuché sur une bataille juridique qui a abouti jusqu'à la Cour suprême. Dans l’affaire de 1921, Hildreth v. Mastoras, il s’agissait de savoir dans quelle mesure un brevet de 1900 pour un tire-tire devait être interprété. C'est-à-dire qu'un modèle ultérieur fabriqué par quelqu'un d'autre constituait-il simplement une amélioration mineure ou s'agissait-il d'un appareil différent? Une partie cruciale de l’argument portait sur la différence entre le brevet de 1900 et le prédécesseur de 1893 (qui n’a probablement jamais été fabriqué). L’avis de la cour, rédigé par le juge en chef William Howard Taft, «témoigne d’une parfaite connaissance de la dynamique topologique», écrit Thiffeault dans son article.
La cour a reconnu que le dispositif précédent - qui ne comportait que deux crochets - n'aurait pas pu étirer la tire au degré exponentiel requis pour une création de confiserie efficace. L'avis de Taft est le suivant:
Avec seulement deux crochets, il ne pouvait y avoir de rodage du bonbon, car il n'y avait pas de troisième épingle pour réengager le bonbon tant qu'il était maintenu entre les deux autres épingles. Le mouvement des deux broches en cercles concentriques pourrait l’étirer un peu et le remuer, mais cela ne le tirerait pas au sens de la technique.
Thiffeault écrit: «L’avis de la Cour suprême montre l’idée fondamentale qu’il faut au moins trois barres pour produire une sorte de croissance rapide.»
Thiffeault dit qu'il existe aujourd'hui deux tire-tire standard, l'un à trois cannes et l'autre à quatre. Ils ont le même facteur d'étirement. Il est lié au soi-disant ratio d'argent, 1+ √2, ou environ 2, 414, un cousin légèrement moins lumineux du nombre d'or plus célèbre.
Le fait que les deux tire-cartouches classiques s’étirent avec le taux d’argent est intéressant, car le taux d’argent est, dans un sens mathématique précis, optimal. Cependant, Thiffeault met en garde qu'il n'est pas si facile de classer les tire-tire différents, même si vous connaissez leurs facteurs d'étirement: «Il y a un aspect pommes et oranges dans lequel il est assez difficile de se déplacer», dit-il. Un extracteur peut avoir plus de tiges et mettre plus de temps à revenir à son état initial qu'un autre, ou peut nécessiter plus de couple ou un engrenage plus complexe. Ainsi, bien que les mathématiques donnent une idée de la qualité de l'extraction des tire-tire, elles ne racontent pas toute l'histoire.
Les recherches de Thiffeault sur les tire-lait l'ont inspiré, ainsi que son étudiant de premier cycle Alex Flanagan, à construire leur propre modèle. Ils voulaient voir s’ils pouvaient augmenter l’efficacité sans trop modifier les engrenages et ont fini par créer un nouvel extracteur à 6 tiges basé sur l’engrenage de l’extracteur à 4 tiges standard. «La raison pour laquelle nous avons pu le faire, c'est que nous avons maintenant des maths», dit Thiffeault. Ils pouvaient modéliser la machine de manière exhaustive sur l'ordinateur et contourner une grande partie des essais et des erreurs avec de véritables dispositifs physiques auparavant inventés par les inventeurs. Le dispositif à 6 barres, qui n’est encore qu’un prototype, étire la tire environ deux fois plus que les extracteurs standard à chaque cycle.
Jusqu’à présent, les fabricants de tire-lait n’avaient pas vraiment cherché à obtenir l’avis de Thiffeault sur l’optimisation de leurs conceptions - Big Taffy est apparemment satisfait de son statu quo extensible - mais il espère que ses méthodes pourraient avoir des effets sur d’autres secteurs. Outre le soufflage du verre, l'industrie pharmaceutique est un lieu logique d'optimisation du mélange. Après tout, le mélange de vitamines et de médicaments nécessite un contrôle de qualité extrêmement élevé: les fabricants sont "disposés à payer beaucoup d'argent pour un mélange parfait" car ils "ne peuvent tolérer qu'une mauvaise multivitamine sur 1 000", déclare Thiffeault. Alors, un jour, les pharmaciens vont peut-être féliciter les dévoués tire-tire d’autrefois.
Là encore, cela pourrait être un peu exagéré.
