Le 14 mars n'est pas un jour de pi ordinaire cette année. Les passionnés de mathématiques célèbrent partout l’événement comme Ultimate Pi Day, car la date correspondra aux cinq premiers chiffres de pi (3, 1415) plutôt qu’aux trois premiers. Cette confluence mathématique ne reviendra pas avant un siècle, le 14 mars 2115.
Contenu connexe
- Le monde est plein de cercles
Défini comme le rapport de la circonférence d'un cercle à son diamètre, pi ( π ) est un nombre transcendantal et irrationnel, ce qui signifie qu'il ne peut jamais être écrit comme le rapport de deux nombres entiers et qu'il continue indéfiniment sans motif répété. Pi n'est pas le seul nombre irrationnel - il y a aussi le nombre d'Euler (e) et le nombre d'or (ou phi), par exemple. Mais il continue d’être une source de fascination car ses origines s’expliquent facilement, explique Mario Livio, astrophysicien à la Space Telescope Science Institute du Maryland.
«Tout le monde peut comprendre comment pi est dérivé. Tous les autres numéros sont plus complexes. Le nombre phi, par exemple, implique une division particulière d'une ligne et le nombre e vous oblige à savoir ce qu'est un logarithme », explique Livio, auteur du livre Is God Mathematician?
Une autre grande partie de l’attrait de pi réside dans le fait qu’elle possède un talent surnaturel pour figurer dans des formules mathématiques, dont beaucoup sont importantes pour les processus quotidiens, du traitement des images à la navigation GPS. Voici juste un petit échantillon des formules couramment utilisées incluant pi:
La transformée de Fourier
Nommé d'après le mathématicien français Jean-Baptiste Joseph Fourier, cet outil mathématique décompose un signal en ses fréquences composantes - un peu comme on peut décomposer un accord musical en ses notes composantes. En fait, les transformées de Fourier sont idéales pour le traitement de signaux basés sur les ondes tels que le son ou la lumière et la recherche de modèles. Cela fait de la transformation de Fourier un outil fondamental du monde numérique moderne.
«C'est ce qu'on appelle l'algorithme le plus important jamais développé par l'humanité. C'est peut-être une hyperbole, mais ce n'est peut-être pas le cas », explique Glen Whitney, fondateur et directeur du Musée national des mathématiques à New York. Les transformées de Fourier sont utilisées tout le temps pour nettoyer les images numériques, pour ajuster automatiquement les stars de la pop et pour rechercher des planètes lointaines en orbite autour d'autres étoiles. Cet outil est également crucial pour les fonctionnalités de synthèse vocale qui sont désormais standard sur les smartphones. «Lorsque vous utilisez Siri ou Google Now, l’une des premières étapes consiste à prendre votre voix et à lui appliquer une transformation de Fourier. Il est beaucoup plus facile de reconnaître les voyelles lorsque vous regardez leurs transformations de Fourier que lorsque vous regardez leurs images. signaux originaux eux-mêmes », dit Whitney.
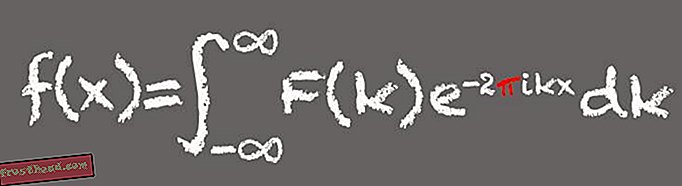(Illustration de Victoria Jaggard) Pi apparaît dans la transformée de Fourier car l’une des composantes ou expressions de la formule est associée à un sinus, un cosinus et aux angles créés par une particule se déplaçant autour d’un cercle. "Chaque fois que vous avez une formule qui traite des cercles ou des angles, vous ne serez pas surpris lorsque pi apparaît", a déclaré Whitney.
Principe d'incertitude de Heisenberg
Le principe d'incertitude de Heisenberg, l'un des piliers de la mécanique quantique, stipule qu'un observateur ne peut pas connaître simultanément la position et la vitesse d'une particule subatomique. Au lieu de cela, plus la position d'une particule est connue avec précision, moins on peut en connaître la vitesse.
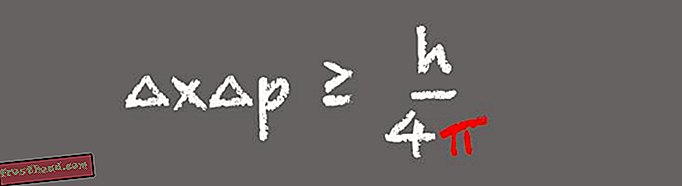(Illustration de Victoria Jaggard) L’apparition de pi dans le principe d’incertitude de Heisenberg prend tout son sens lorsque vous réalisez que, dans la formule, la position et l’élan sont des transformations de Fourier les unes des autres, explique Whitney. Le principe d'incertitude est important dans le monde moderne, car il décrit le comportement des particules lumineuses, ou photons, dans les systèmes de communication à fibres optiques. «Cela nous dit que nous ne pouvons pas connaître à la fois la position et l’élan des photons avec une précision extrême. Vous ne pouvez pas concevoir de protocoles de communication qui violent le principe d'incertitude de Heisenberg, car ils ne fonctionneront pas. "
Loi de Stoke
La loi de Stoke calcule la force nécessaire pour déplacer une petite sphère, c'est-à-dire un cercle tridimensionnel, à travers un fluide visqueux à une certaine vitesse. Il a des applications dans des domaines allant des sciences de la Terre à la médecine.
(Illustration de Victoria Jaggard) «La loi concerne spécifiquement l'effet de la viscosité sur une sphère dans le fluide», explique Whitney. C'est ainsi que pi entre en jeu. En ce qui concerne les utilisations pratiques de la loi de Stoke, ne cherchez pas plus loin que votre voiture. «Pendant des décennies, les entreprises ont veillé à ce que votre huile moteur ait la viscosité appropriée. Une série de sphères d’essai a littéralement été déposée sur l’huile et le temps qu’il a fallu pour passer à travers le liquide», a déclaré Whitney. Aujourd'hui, la méthode la plus courante pour mesurer la viscosité de l'huile consiste à utiliser un outil appelé viscosimètre à tube capillaire. Aucune sphère n'est nécessaire, mais le résultat est toujours présenté en unités de mesure, appelées centistokes.
Formule d'Euler
Nommé d'après le mathématicien suisse Leonard Euler, la version de cette formule qui inclut pi regroupe en un seul endroit quelques-uns des nombres les plus intrigants en mathématiques:
(Illustration de Victoria Jaggard) «Tout le monde pense que c'est incroyable. Tous ces chiffres que nous considérons comme spéciaux apparaissent dans une belle équation », déclare Livio. Bien que cette formule complexe puisse inspirer l’impression des mathématiciens, la forme la plus utile de l’équation est légèrement plus longue:
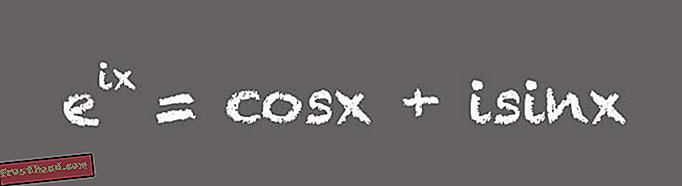(Illustration de Victoria Jaggard) Cette version décompressée de la formule d'Euler est un outil incroyable, déclare Whitney. Par exemple, il est important de concevoir des composants électroniques utilisant le courant alternatif ou le courant alternatif. «La formule d'Euler, dans sa forme développée, signifie que vous pouvez utiliser des nombres complexes ou imaginaires pour analyser et concevoir des circuits de courant alternatif», déclare Whitney. En effet, dans un circuit à courant alternatif, la tension est une quantité qui oscille dans le temps, généralement 60 fois par seconde, par exemple dans l’alimentation électrique standard des États-Unis. «La version complète de la formule d'Euler enseigne comment utiliser les nombres complexes comme un raccourci pratique pour modéliser des phénomènes oscillants», explique Whitney.
Équations de terrain d'Einstein
Composante essentielle de sa théorie de la relativité générale, les équations de champ d'Albert Einstein décrivent comment la gravité à partir de la masse et de l'énergie crée la courbure de l'espace-temps.
(Illustration de Victoria Jaggard) «Décrire que la courbure implique la géométrie, et puisque la définition originale de pi vient de la géométrie, son apparence dans cette équation n’a rien d’étonnant, a déclaré Livio. En plus de révéler une vérité fondamentale sur le fonctionnement de l'univers, la relativité générale a de nombreuses applications pratiques. Par exemple, les satellites qui composent le système de positionnement global utilisé pour la navigation seraient désespérément désynchronisés les uns des autres si les ingénieurs ne prenaient pas en compte les effets de dilatation du temps prédits par la théorie.
