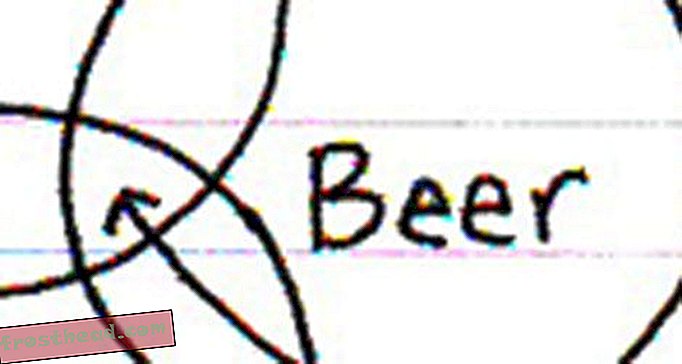Vous avez probablement rencontré des objets unilatéraux des centaines de fois dans votre vie quotidienne - comme le symbole universel du recyclage, qui se trouve imprimé sur le dos de canettes d'aluminium et de bouteilles en plastique.
Cet objet mathématique s'appelle une bande de Mobius. Il a fasciné les environnementalistes, les artistes, les ingénieurs, les mathématiciens et bien d’autres depuis sa découverte en 1858 par August Möbius, un mathématicien allemand décédé il y a 150 ans, le 26 septembre 1868.
Möbius découvrit la bande unilatérale en 1858 alors qu'il était président de l'astronomie et de la mécanique supérieure à l'Université de Leipzig. (Un autre mathématicien nommé Listing l'a décrit quelques mois plus tôt, mais n'a publié son travail qu'en 1861.) Möbius semble avoir rencontré la bande de Möbius alors qu'il travaillait sur la théorie géométrique des polyèdres, des figures pleines composées de sommets, d'arêtes et de faces planes. .
Une bande de Möbius peut être créée en prenant une bande de papier, ce qui lui donne un nombre impair de demi-tours, puis en recollant les extrémités pour former une boucle. Si vous prenez un crayon et tracez une ligne le long du centre de la bande, vous verrez que la ligne s'étend apparemment des deux côtés de la boucle.
Le concept d'objet unilatéral a inspiré des artistes tels que le graphiste néerlandais MC Escher, dont la gravure sur bois «Möbius Strip II» représente des fourmis rouges rampant les unes après les autres le long d'une bande de Möbius.
La bande de Möbius a plus d'une propriété surprenante. Par exemple, essayez de prendre une paire de ciseaux et de couper la bande en deux le long de la ligne que vous venez de dessiner. Vous serez peut-être étonné de constater que vous ne vous retrouverez plus avec deux bandes Möbius unilatérales plus petites, mais avec une longue boucle bilatérale. Si vous n'avez pas de papier sous la main, la gravure sur bois «Möbius Strip I» d'Escher montre ce qui se produit lorsqu'une bande de Möbius est coupée le long de son axe.
Si la bande présente un attrait visuel certain, son impact le plus important a été en mathématiques, où elle a permis de stimuler le développement de tout un domaine appelé topologie.
Un topologue étudie les propriétés des objets conservés lorsqu’ils sont déplacés, pliés, étirés ou tordus, sans couper ni coller des pièces ensemble. Par exemple, une paire d’embouts enchevêtrés est topologiquement identique à une paire d’embouts enchevêtrés, car le passage d’un embout à l’autre ne nécessite que le déplacement, la flexion et la torsion. Aucune coupe ou collage n'est nécessaire pour transformer entre eux.
Une autre paire d'objets qui sont topologiquement identiques est une tasse à café et un beignet. Étant donné que les deux objets ne possèdent qu'un seul trou, l'un peut être déformé en un autre par simple étirement et flexion.
 Une tasse se transforme en beignet. (Wikimedia Commons)
Une tasse se transforme en beignet. (Wikimedia Commons) Le nombre de trous dans un objet est une propriété qui ne peut être changée que par découpage ou collage. Cette propriété - appelée le "genre" d'un objet - nous permet de dire qu'une paire d'écouteurs et un beignet sont topologiquement différents, puisqu'un beignet a un trou, alors qu'une paire d'écouteurs n'a pas de trous.
Malheureusement, une bande de Möbius et une boucle à deux côtés, comme un bracelet de sensibilisation en silicone typique, semblent avoir un seul trou, cette propriété est donc insuffisante pour les différencier - du moins du point de vue d'un topologue.
Au lieu de cela, la propriété qui distingue une bande de Möbius d'une boucle à deux côtés est appelée orientabilité. Comme son nombre de trous, l’orientabilité d’un objet ne peut être modifiée que par découpage ou collage.
Imaginez-vous écrire une note sur une surface transparente, puis vous promener sur cette surface. La surface est orientable si, lorsque vous revenez de votre promenade, vous pouvez toujours lire la note. Sur une surface non orientable, vous pouvez revenir de votre promenade uniquement pour constater que les mots que vous avez écrits se sont apparemment transformés en image miroir et ne peuvent être lus que de droite à gauche. Sur la boucle bilatérale, la note sera toujours lue de gauche à droite, quel que soit le lieu de votre voyage.
Comme la bande de Möbius est non orientable, alors que la boucle à deux côtés est orientable, cela signifie que la bande de Möbius et la boucle à deux côtés sont topologiquement différentes.
 (Créé par David Gunderman)
(Créé par David Gunderman) Lorsque le fichier GIF démarre, les points énumérés dans le sens des aiguilles d’une montre sont les points noir, bleu et rouge. Cependant, nous pouvons déplacer la configuration à trois points autour de la bande de Möbius de telle sorte que la figure se trouve au même endroit, mais les couleurs des points énumérés dans le sens des aiguilles d'une montre sont maintenant le rouge, le bleu et le noir. D'une manière ou d'une autre, la configuration est devenue sa propre image miroir, mais tout ce que nous avons fait est de la déplacer à la surface. Cette transformation est impossible sur une surface orientable comme la boucle à deux côtés.
Le concept d’orientabilité a des implications importantes. Prenez des énantiomères. Ces composés chimiques ont les mêmes structures chimiques, à une différence essentielle près: ils sont des images inversées les uns des autres. Par exemple, la substance chimique L-méthamphétamine est un ingrédient des inhalateurs à vapeur de Vicks. Son image miroir, la D-méthamphétamine, est une drogue illicite de classe A. Si nous vivions dans un monde non orientable, ces produits chimiques seraient indiscernables.
La découverte d'August Möbius a ouvert de nouvelles voies pour étudier le monde naturel. L'étude de la topologie continue de produire des résultats étonnants. Par exemple, l'an dernier, la topologie a conduit les scientifiques à découvrir d'étranges nouveaux états de la matière. La médaille Fields de cette année, la plus haute distinction en mathématiques, a été remise à Akshay Venkatesh, une mathématicienne qui a aidé à intégrer la topologie à d'autres domaines, tels que la théorie des nombres.
Cet article a été publié à l'origine sur The Conversation.
David Gunderman, Ph.D. étudiant en mathématiques appliquées à l'Université du Colorado et Richard Gunderman, professeur chancelier de médecine, arts libéraux et philanthropie à l'Université d'Indiana